In Distilling the Knowledge in a Neural Network paper, there is described how soft targets of the final softmax layer can be modified by additional denominator called temperature. This blog posts aims to visualize effect of temperature magnitude on output of modified softmax layer.

Our more general solution, called “distillation”, is to raise the temperature of the final softmax until the cumbersomemodel produces a suitably soft set of targets. We then use the same high temperature when training the small model to match these soft targets. We show later that matching the logits of the cumbersome model is actually a special case of distillation.

https://arxiv.org/abs/1503.02531

Temperature

%matplotlib inline

import numpy as np
import matplotlib
import numpy as np
import matplotlib.pyplot as plt

def softmax(logits, T=1):
    logits_temperature = np.exp(logits/T)
    return logits_temperature/np.sum(logits_temperature, axis=1)

def softmax_temperature_test(L, T):
    S = softmax(L, T)
    print(S)
    plt.bar(range(len(S[0])), S[0])

Logits

L = np.array([[10, 20, 30]])

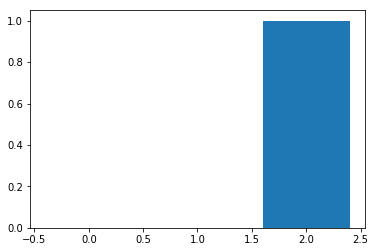
T = 1

softmax_temperature_test(L, T=1)

[[  2.06106005e-09   4.53978686e-05   9.99954600e-01]]

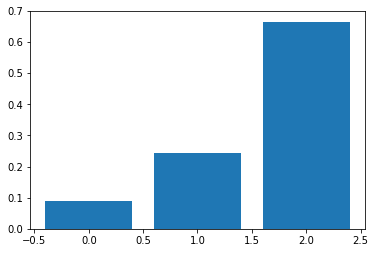
T = 10

softmax_temperature_test(L, T=10)

[[ 0.09003057  0.24472847  0.66524096]]

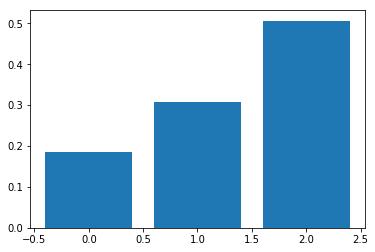
T = 20

softmax_temperature_test(L, T=20)

[[ 0.18632372  0.30719589  0.50648039]]

T = 30

softmax_temperature_test(L, T=30)

[[ 0.23023722  0.32132192  0.44844086]]

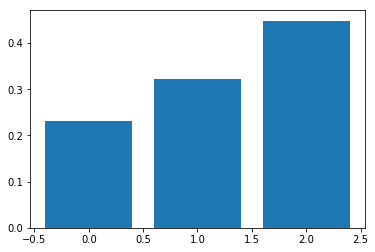
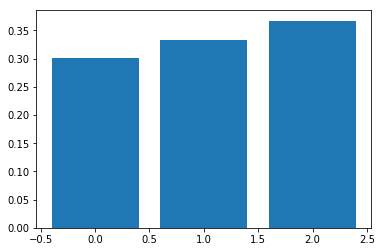
T = 100

softmax_temperature_test(L, T=100)

[[ 0.30060961  0.33222499  0.3671654 ]]